Asynchronous, event-based artificial retinas¹ are introducing a shift in current methods of tackling visual signal processing.^2–4 Conventional frame-based image acquisition and processing technologies are not designed to take full advantage of the dynamic characteristics of visual scenes. A collection of snapshots is static and contains much redundant information. That is because every pixel is sampled repetitively, even if its value is unchanged, and thus unnecessarily digitized, transmitted, and finally stored.⁵ This waste of resources significantly limits memory and computational time in computer vision applications.

Event-based dynamic vision sensors (DVSs)⁶ provide a novel and efficient way of encoding light and its temporal variations by asynchronously reacting and transmitting only the scene changes at the exact time they occur.^{5, 7–14} This is similar to retinal outputs, which are massively parallel, asynchronous, and data-driven according to the information retrieved in scenes.¹⁵

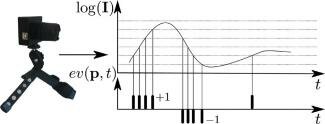
Here, we describe work on time-oriented computation of 3D information^2,3 that introduces event-based computation into computer vision techniques such as calibration and stereo matching. This approach uses two DVS models⁵ whose acquisition principle is shown in Figure 1. The DVS models the transient responses of the retina,¹⁶ uses an address-event representation with 128×128 pixels, and has an output of asynchronous address events that signal scene-reflectance changes as they happen. Each pixel is independent and detects changes in log intensity larger than a threshold since the last event emitted (typically 15% contrast). When the change in log intensity exceeds a set threshold, a signed event is generated by the pixel depending on whether the log intensity increased or decreased. Since the DVS is not clocked like conventional cameras, the timing of events can be conveyed with a very high temporal resolution of approximately 1μs. Thus, the frame rate is typically several kilohertz. The stream of events from the retina can be −1 or +1 polarity when a negative or a positive contrast change is detected. The absence of events when no contrast change is detected implies that redundant visual information usually recorded in frames is not carried in the stream of events.

Left: The dynamic vision sensor (DVS) silicon retina. Right: Adapted principle of DVS pixel event generation. Events with +1 or - 1 polarity are emitted when the change in log intensity exceeds a predefined threshold. I: Intensity. ev: Event. p: Pixel. t: Time.

The aim of stereovision is to compute depth using two sensors viewing the scene from different positions. In this context, two elementary steps are typically performed, calibration and matching. Calibration allows estimation of the pose between the two sensors of a stereovision acquisition chain. Once a match between two views has been identified, calibration provides all the information needed to estimate the position in the observed point's 3D space. Calibration is performed only once at the beginning of the process, unless the relative position of the sensors is changed. Matching allows identification of scene point projections in two images. In the frame-based case, matching relies on neighboring gray level similarities. Two pixels are matched if their neighborhoods are similar.

Principle of epipolar geometry in stereovision. With two geometrically related images, the epipolar relation is given by the fundamental matrix that associates to each point p(left) the set of its possible corresponding matched points (right), in this case is a line l. Point p ^′ is the match of p, and then belongs to l. The fundamental matrix Fis a 3×3 matrix such as l=Fp.

The fundamental matrix relates corresponding points in stereo images. It contains the geometric relations between the 3D points and their projections onto the 2D images of each acquired scene view.¹⁷The fundamental matrix associates to an image point p (expressed as a homogeneous vector of size 3×1 in a 2D projective space) a line l in the right image that can be computed as l=Fp (see Figure 2). This line contains all points that can possibly match with p, and it represents the line of sight of pixel p in the right image. If p ′ is the match of p, the fundamental matrix satisfies p ′ ^TFp=0.

If eight-point matches are known, the fundamental matrix is the solution of a set of linear equations.¹⁸ Otherwise, it can be found by solving a linear least-squares minimization problem. With enough matched pairs p ′ ↔p, equation p ′ ^TFp=0 can be used to compute the unknown matrix F. Each point match gives rise to one linear equation in the unknown entries of F. From all the point matches, we obtain a set of linear equations of the form Af=0, where f is a 9-vector containing the entries of the matrix F, and A is the equation matrix.

Experimental setup with the two DVS retinas placed in front of an LED-lit liquid crystal display screen. The screen's position was changed to provide several levels of depth. For each screen position, the probability coactivation field was computed. C₁, C₂: Retinas. P₁, P₂: Events.

We let two asynchronous, event-based DVS sensors observe a common part of a scene (see Figure 3). A 3D point P moving in space triggers changes of luminance in the sensors' common field of view. The 3D point generates two events, p₁ and p₂, at very close timings, respectively, in retinas C₁ and C₂. In an ideal case, the set of corresponding events should be time-stamped with equal values, as they are the consequence of the same event that happens at a given time. Unfortunately, due to latencies in the acquisition system, the two events will not be generated at the same time.

The idea is then to follow the activity of a single pixel. If p₂ is the pixel to be monitored in the left retina C₂, we can estimate which pixels of the right retina C₁ are active in a temporal interval around each activation of p₂. This activation monitoring provides a coactivation probability measure for each pixel of C₁. The probability will obviously depend on the geometric link between the pixels' line of sight. Pixels that see the same thing at the same time have a high probability of being coactive. The probability activation map of all the pixels of C₁ contains geometrical information on F. Pixels of C₁ that tend to be active with p₂ must lie along the epipolar line Fp₂.

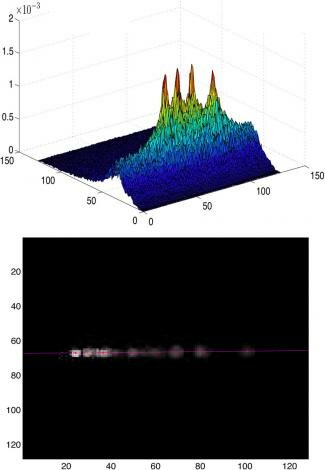
The experimental results of monitoring clearly show that the highest coactivation probabilities lay on a line that corresponds to the epipolar line of the left retina's selected pixel (see Figure 4).

Top: Coactivation probability map of a pixel using four screen positions. Bottom: The high-probability corresponding active pixels all lie on the epipolar line.

It is interesting to notice that the fundamental matrix appears implicitly from the coactivation of pixels. There is no need to define or match any pattern in the observed scenes. This is an unusual estimation process of the epipolar geometry. The fundamental matrix is the result of temporal coactivation of pixel activities and can therefore be considered a Hebbian fundamental matrix. This process can be performed for all the pixels of C₁, thus providing the geometric link between the two retinas.

Once the epipolar geometry has been estimated, it is possible to start the event-matching step. Although the exact timing or close to exact timing cannot be used to discriminate the matches, it is possible to define a time window in which true matches are more likely to occur.

The idea is to use the distance to their corresponding epipolar lines of possible matching events occurring at the same time. F links C₂ to C₁, and a point p²₁ appearing in retina C₂ provides a line l₂₁ in C₁ using Fp²₁=l₂₁. The epipolar line l₂₁ contains all possible matches of the event occurring at the spatial location p¹₁ in C₂ (see Figure 5).

Two events generated by the scene point P at time twill be detected by corresponding pixels located at p¹₁and p²₁ at slightly different times. There are only a few possible candidates matching the event if the distance to the epipolar line land a time window around t are used.

We implemented the stereo matching algorithm in the open-source Java software project. We generated disparity maps from the events by moving a pen back and forth at three different distances from the two retinas separated by about 10cm. The computed disparity is color-coded from blue to red for results varying between 0 and 127 pixels, respectively. The default value for background unprocessed pixels is 0. The matching used a time window of 1ms and a maximum distance to the epipolar line of 1 pixel. The disparity is a decreasing function of the depth. Some pixels are not matched due to multiple matching.

In summary, we have described an event-based stereo chain. We have shown that the asynchronous high temporal resolution properties of event-based acquisition are particularly efficient in terms of computational load and accuracy. The sparse nature of the acquired signals allows exploration of new paradigms for time-oriented computer vision. The entirely event-driven algorithm of stereo vision takes full advantage of the data-driven neuromorphic signal. The combination of spatial and temporal constraints fully uses the high temporal resolution of neuromorphic retinas. Asynchronous event-based acquisition is a promising 3D technology offering yet unexplored potential to overcome the current limitations of frame-based 3D vision. These sensors should be of great use to the robotics and computer vision communities, especially for embedded computer vision applications. This technology will attract greater interest once retinas with larger spatial resolutions are available. We are currently extending this work to multicamera networks for real-time 3D streaming.

2. T. Delbruck, B. Linares-Barranco, E. Culurciello and C. Posch, Activity-driven event-based vision sensors, IEEE Int'l Symp. Circuits Syst., pp. 2, 2010.
   
   
3. P. Rogister, R. Benosman, S. Ieng, P. Lichtsteiner and T. Delbruck, Asynchronous event-based binocular stereo matching, IEEE Trans. Neural Networks, 2011.
   
   
4. R. Benosman, S. Ieng, C. Clercq, C. Bartolozzi and M. Srinivasan, Asynchronous frameless event-based optical flow, Neural Networks, 2012.
   
   
5. R. Benosman, S. Ieng, C. Posch and P. Rogister, Asynchronous event-based Hebbian epipolar geometry, IEEE Trans. Neural Networks, 2011.
   
   
6. P. Lichtsteiner, C. Posch and T. Delbruck, A 128 × 128 120dB 15μs latency asynchronous temporal contrast vision sensor, IEEE J. Solid-State Circuits 43 (2), pp. 566-576, 2008.
   
   
7. C. Mead, Adaptive retina, Analog VLSI Implementation of Neural Systems, 1989.
   
   
8. C. Posch, High-DR frame-free PWM imaging with asynchronous AER intensity encoding and focal-plane temporal redundancy suppression, IEE Int'l Symp. Circuits and Syst., 2010.
   
   
9. P. Lichtsteiner, T. Delbruck and J. Kramer, Improved on/off temporally differentiating address-event imager, Proc. 11th IEEE Int'l Conf. Electron. Circuits Syst., pp. 211-214, 2004.
   
   
10. K. A. Zaghloul and K. Boahen, Optic nerve signals in a neuromorphic chip II: testing and results, Trans. Bomed. Eng. 51 (4), pp. 667-675, 2004.
    
    
11. P.-F. Ruedi, P. Heim, F. Kaess, E. Grenet, F. Heitger, P.-Y. Burgi, S. Gyger and P. Nussbaum, A 128×128 pixel 120 dB dynamic range vision sensor chip for image contrast and orientation extraction, Proc. Int'l Solid-State Circuits Conf., pp. 226-490, 2003.
    
    
12. P. Lichtsteiner, C. Posch and T. Delbruck, A 128 × 128 120db 30mW asynchronous vision sensor that responds to relative intensity change, Proc. IEEE Int'l Solid-State Circuits Conf., pp. 2, 2006.
    
    
13. U. Mallik, M. Clapp, E. Choi, G. Cauwenberghs and R. Etienne-Cummings, Temporal change threshold detection imager, Proc. Int'l Solid-State Circuits Conf., pp. 362-603, 2005.
    
    
14. E. Culurciello and R. Etienne-Cummings, Second generation of high dynamic range, arbitrated digital imager, Proc. Int'l Symp. Circuits Syst., 2004.
    
    
15. T. Delbruck and P. Lichtsteiner, Fast sensory motor control based on event-based hybrid neuromorphic-procedural system, IEEE Int'l Symp. Circuits Syst., pp. 845-849, 2007.
    
    
16. B. Roska, M. Alyosha and F. Werblin, Parallel processing in retinal ganglion cells: how integration of space-time patterns of excitation and inhibition form the spiking output, J. Neurophysiol. 95 (6), pp. 3, 2006.
    
    
17. B. Roska and F. Werblin, Rapid global shifts in natural scenes block spiking in specific ganglion cell types, Nat. Neurosci. 6, pp. 600-608, 2003.
    
    
18. R. Hartley and A. Zisserman, Multiple View Geometry in Computer Vision, Cambridge University Press, 2003.
    
    
19. R. Hartley, In defense of the eight-point algorithm, IEEE Trans. Pattern Anal. Machine Intell. 19, pp. 580-593, 1997.